Hier wird nicht Mathematik gelehrt, sondern ein Ersatz
Ein Gastbeitrag von Prof. em. Hermann Karcher
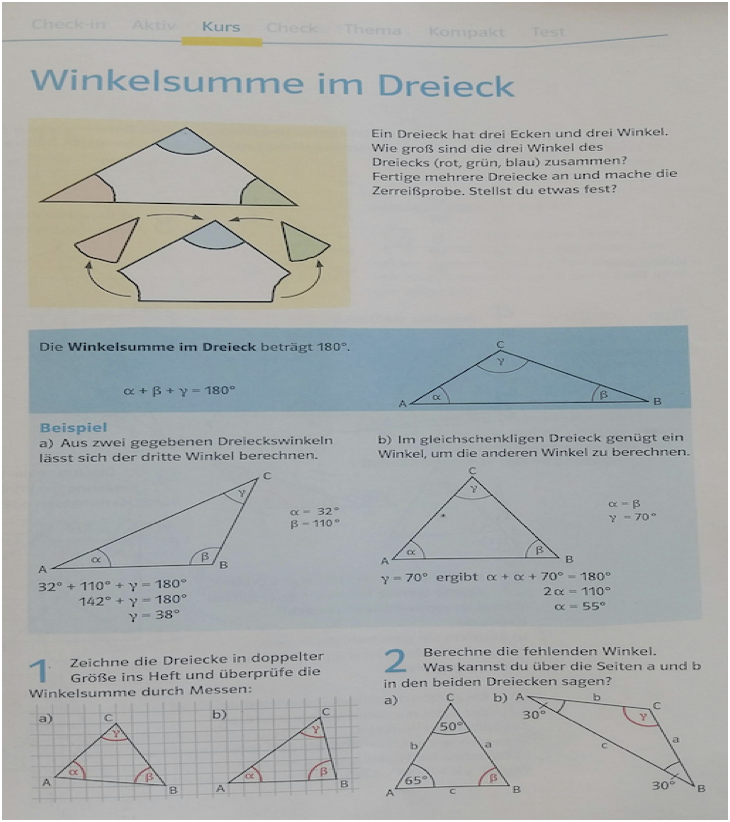
So wird die Winkelsumme im Dreieck in einem aktuellen Schulbuch eingeführt. In diesem Beispiel wird die Mathematik behandelt, als wäre sie eine Erfahrungswissenschaft: Als könnten die Schüler, wenn sie nur oft genug Dreiecken die Ecken abreißen, irgendwann „beweisen“, dass die drei aneinandergelegten Winkel zusammen eine durchgehende gerade Kante bilden und daher die Summe von 180° haben. Das ist aber kein mathematischer Beweis, eine sichere Erkenntnis, dass das immer so ist, kann man so nicht gewinnen. Es ist wie mit den Kleeblättern: Die sind dreiblättrig – immer?
Ein Rückgriff auf die mathematischen Vorkenntnisse der Schüler erfolgt im Buch nicht. Stattdessen wird sofort mit der rezeptartigen Anwendung dieser “Entdeckung” fortgefahren. Dabei stünden den Schülern eigentlich genug Vorkenntnisse zur Verfügung, um auf genuin mathematische Weise diese Entdeckung wirklich selbst zu machen. Danach könnte man so fortfahren:
Beweis aus der Winkelsumme im Rechteck
Laut Lehrplan gehören Rechtecke mit ihren Diagonalen zu den ersten geometrischen Figuren, die die Schülerinnen und Schüler kennen lernen. Die Winkelsumme im Rechteck ergibt vier rechte Winkel (360 Grad),
eine Diagonale zerlegt das Rechteck in zwei gleiche Dreiecke. Deren Winkelsumme ist also die Hälfte von 360 Grad. So könnte man zeigen, dass die Winkelsumme im rechtwinkligen Dreieck immer 180 Grad betragen muss, denn ein rechtwinkliges Dreieck ist immer ein halbes Rechteck.
Zweiter Beweisteil durch Zerlegung nicht rechtwinkliger Dreiecke
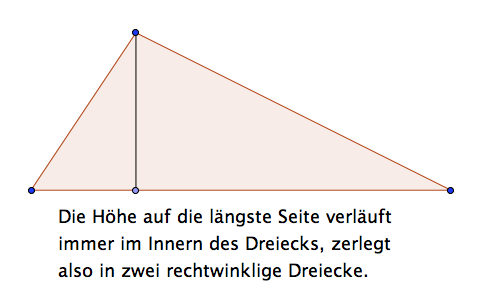
Man kann nun so fortfahren: Beliebige Dreiecke können durch die Höhe auf der längsten Seite in zwei rechtwinklige Dreiecke zerlegt werden.
Die beiden rechtwinkligen Teildreiecke haben eine Winkelsumme von 2×180° und die Summe ihrer spitzen Winkel ist gleich der Winkelsumme des ursprünglichen Dreiecks, also wieder 180 Grad. Auch auf diese Weise könnte man besser als durch das Abreißen von Papierecken zeigen, wie sich die Winkelsumme von 180 Grad schlüssig begründen lässt.
Es übt den Umgang mit logischen Argumenten, wenn man in ähnlichen Situationen auf dieselbe Weise zum Ziel kommt. Laut Lehrplan kennen die Schüler zu diesem Zeitpunkt auch schon parallele Geraden und Stufenwinkel an Parallelen. Daraus folgt eine weitere Erklärung für den Winkelsummensatz:
Beweis über Stufen- und Wechselwinkel
Benachbarte Winkel eines Parallelograms haben die Summe 180 Grad, d.h. auch die Winkelsumme des Parallelograms ist 360 Grad. Wieder zerlegt jede Diagonale das Parallelogram in zwei gleiche Dreiecke, jedes mit Winkelsumme 180 Grad. Der Beweis über Stufen- und Wechselwinkel wäre zum Zeitpunkt, an dem die oben abgebildete Buchseite eingesetzt wird, ebenfalls bereits möglich. Da jedes Dreieck zu einem Parallelogramm verdoppelt werden kann, braucht man das Zerschneiden in rechtwinklige Dreiecke hier nicht mehr.
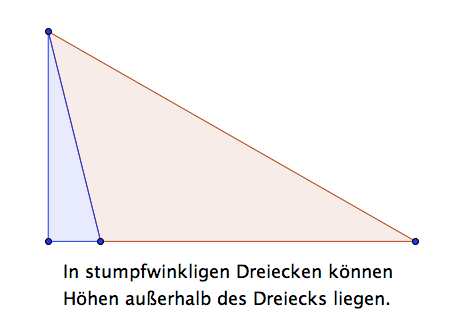
Zu dem ersten Beweis kann man noch die Zusatzfrage stellen: „Kann man auch die ausserhalb eines stumpfwinkligen Dreiecks liegenden Höhen benutzen, um aus der Winkelsumme rechtwinkliger Dreiecke auf die Winkelsumme des stumpfwinkligen Dreiecks zu schließen?“
Das führt hier aber zu weit. Worum es geht, ist der unnötige Verzicht auf logische, mathematische Argumentation.
Es ist weder notwendig noch hilfreich, auf logische Argumentation zu verzichten
Ein wesentlicher Grund dafür, dass die Mathematik zentrales Werkzeug der exakten Naturwissenschaften ist, liegt daran, dass jede Generation auf den Ergebnissen der früheren Generationen aufbauen kann. Das wird dadurch möglich, dass die Mathematik nicht eine beobachtende, sondern eine logisch argumentierende Wissenschaft ist. Bekanntlich sah selbst Newton sich auf den Schultern von Giganten stehend. Die in dem Schulbuch vorgeführte Verweigerung logischer Argumente bedeutet, dass nicht mehr Mathematik, sondern eine Ersatzerfindung der Autoren gelehrt wird. Das ist völlig überflüssig, selbst dreijährige Kindern verblüffen ihre Eltern gelegentlich, wenn sie ein logisches Argument zum eigenen Vorteil einsetzen…
So wäre die Winkelsumme im rechtwinkligen Dreieck für die Schüler verständlich allgemeingültig begründbar und nicht durch eine Beobachtung am Einzelfall. Diese Begründung wäre im Gegensatz zur reinen Beobachtung eine mathematische – sie würde diesem Fach gerecht und lieferte den Schülern Sicherheit.

